Exercice théorème de thévenin et Théorème de Superposition exo+corrigés

Théorème de Superposition et théorème de thévenin

Exercice 1

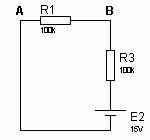
Utiliser le théorème de superposition pour calculer le courant qui circule dans R3

Exercice 2

Utiliser le théorème de superposition pour calculer la tension U_AB aux bornes de R1.

Exercice 3

Utiliser le théorème de superposition pour calculer la tension aux bornes de R1.

Exercice 4

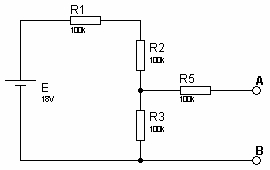
1. Dessinez le générateur de Thévenin de la figure suivante, sans tenir compte de la résistance R.

2. pour R = 150 kΩ

      a. Déterminez le courant qui traverse R

      b. calculer la puissance fournie à R

Exercice 5

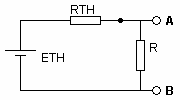
Déterminer les caractéristiques ET et RT du générateur de Thévenin équivalent au circuit suivant, sans tenir compte de la résistance R.

Exercice 6

Dans le montage suivant, déterminer le courant I circulant dans la résistance R = 100k.

Exercice 7

1. Dessinez le générateur de Thévenin de la figure suivante, sans tenir compte de la résistance R.

2. Calculez la tension UR et la puissance fournie à la résistance R.

Exercice 8

Dessinez le générateur de Thévenin de la figure suivante, sans tenir compte de la résistance R.

------------------------------------------------------------------------------------------------

CORRECTION - SOLUTIONS

------------------------------------------------------------------------------------------------

Solution Exercice 1

Pour calculer le courant qui circule dans R3, on calcule la tension aux bornes de R3.

fig1

fig2

1- on calcule la tension U’ (aux bornes de R3) avec E2 en court-circuit (fig1)

U’ = E1 x (R2 // R3) / [(R2 // R3) + R1] = 15V x 50 / 150 = 5V

2- on calcule la tension U’’ (aux bornes de R3) avec E1 en court-circuit (fig2)

U’’ = -E2 x (R1 // R3) / [(R1 // R3) + R2] = -12V x 50 / 150 = -4V

3- la tension U aux bornes de R3 est : U = U’ + U’’ = 1V

4- I = U / R3 = 1V / 100k = 10μA

Solution Exercice 2

fig3

fig4

1- on calcule la tension U’AB avec E2 en court-circuit (fig3)

U’AB = E1 x R1 / [R3 + R1] = 12V x 100 / 200 = 6V

2- on calcule la tension U’’AB avec E1 en court-circuit (fig4)

U’’AB = - U’’BA = -E2 x R1 / [R1 + R3] = -15V x 100 / 200 = -7,5V

3- UAB = U’AB + U’’AB = 6V – 7,5V = 1,5V

Solution Exercice 3

fig5

fig6

1- on calcule la tension U’ avec le générateur de courant ouvert (fig5)

U’ = E1 x R1 / [R1 + R2 + R3] = 15V x 10 / 20 = 7,5V

2- on calcule la tension U’’ avec E en court-circuit (fig6)

U’’ = I1 x R1 = I2 x (R2 + R3) = I x R1 // (R2 + R3) = 1mA x 10 x 10 / (10 +10) = 5V

3- U = U’ + U’’ = 7,5V + 5V = 12,5V

Solution Exercice 4

fig7

fig8

1. Eth = UAB = E x R3 / ( R1 + R2 + R3) = 18 x 100 / (100 + 100 + 100) = 6V

Rth = RAB = R5 + R3 // (R2 + R1) = 100k + 100k x 200k / 300k = 166,67k

2. pour R = 150 kΩ

a. I = Eth / (Rth + R) = 18,95μA

b. P = R x I2 = 53,85μW

Solution Exercice 5

1. on calcule Eth = UAB

R6 = R2 + R3 // R4 = 50k +100k //100k = 100k

Eth = UAB = E x (R5 // R6) / [R1 + (R5 // R6)] = 15V x 50k / 100k = 7,5V

2. on calcule Rth = RAB

Rth = RAB = R1 // R5 // R6 = 25k

Solution Exercice 6

1. on calcule Eth = UAB et Rth = RAB

Eth = UAB = UA - UB

UA = E x R2 / (R1 +R2) = 10V x 100 / 200 = 5V

UB = E x R5 / ( R3 + R4 + R5)

UB = 10V x 25 / 100 = 2,5V

Eth = UAB = UA - UB = 5V – 2,5V = 2,5V

Rth = RAB = (R1 // R2) + [R5 // (R3+R4)] = 100k // 100k + 25k // 75k = 50k + 18,75k = 68,75k

2. pour R = 100 k I = Eth / (Rth + R) = 2,5V / (68,75k + 100k) = 14,81μA

Solution Exercice 7

1. on calcule Eth = UAB et Rth = RAB

Eth = UAB = UA - UB

UA = E1 x R2 / (R1 +R2) = 12V x 100 / 200 = 6V

UB = E2 x R4 / (R3 + R4) = 5V x 100 / 200 = 2,5V

Eth = UAB = UA - UB = 6V – 2,5V = 3,5V

Rth = RAB = (R1 //R2) + (R3 // R4) = 100k // 100k +100k // 100k = 100k

2. UR = Eth x R / (Rth + R) = 3,5V x 100k / (100k + 100k) = 1,75V

PR = UR

2 / R = (1,75V) 2 / 100k = 30,625μW

Solution Exercice 8

1. on calcule Eth = UAB

On utilise la transformation triangle-étoile. Puisque R2 = R3 = R4 = 33k, RA = RB = RC = 33k / 3 = 11k

Eth = UAB = E x (R1 + RA) / (R1 + RA + RB) = 10V x (22k + 11k) / (22k + 11k +11k) = 7,5V

2. on calcule Rth = RAB

Rth = RAB = [(R1 + RA) // RB] + RC = 33k // 11k + 11k = 19,25k

3.